0.01を10000回の件、
・倍精度浮動小数点のバイナリ配置を言える者が笑いなさい
・桁落ちしない計算手法を提示できる者が石を投げなさい— Tomoaki Masuda (@moonmile) 2018年11月18日
元ネタの引用リツイートが3件ほど立て続けてに回ってきたのと、「俺たちはテストコードにいつまで ε を書かないといけないのだろうか?」というツイートがあったので、それを絡めて。
最初に TDD の話だけ書いておこう(一連のツイートには書かなかったので)。
xUnit のテストコードに誤差範囲を指定する
自動単体テストでは、Assert.AreEqual( 期待値, 実測値 ) な形で、数値や文字列を比較するけど、これ実数(double)の場合は、Assert.AreEqual( 期待値, 実測値, 誤差 ) という形で誤差の許容範囲を指定しないといけない。これ、文字列や整数値に場合にはピッタリ一致するのだけど、実数の場合はそうはいかない。科学計算のユニットテストを書くとわかるが、計算順序や計算の精度などを上げると、微妙に値がずれる。そのたびにいちいち期待値を変えていられない、というか期待値を変えてしまってはテストコードにならないので、許容範囲を指定する。大抵の場合は有効桁数を書くことになるので、
Assert.AreEqual( 100.00, 実測値, 0.01)
な形で有効桁数を示すことが多い。この場合は、99.99001(99.99より大きい) から 100.00999…(100.01より小さい) を 100.00 と扱うことができる。不等号を使えば、
99.99 < 実測値 < 100.01
の範囲となる。両端を含まない「開区間」になるんだが、まあ細かいことはどうでもいい(本当は重要だけど)。こんな感じで真の値から幅のある値を取る。
コンピュータで扱う実数とは何か?
知識として整数値(int型)と実数値(doubleやfloat)を分けてコーディングをしないといけない、というのは知っている人が多いと思うのだけど、じゃあ double や float を使う場合、コンピュータ上でどう扱っているのか?というのを知っている人は…理/工学系には「教養」だよ!という話だったりする。
倍精度浮動小数点数 – Wikipedia https://ja.wikipedia.org/wiki/%E5%80%8D%E7%B2%BE%E5%BA%A6%E6%B5%AE%E5%8B%95%E5%B0%8F%E6%95%B0%E7%82%B9%E6%95%B0

倍精度の「倍」の意味は、単精度の倍だから。なので、単精度が32ビット、倍精度が64ビットになる。8の倍数になっているのはコンピュータで扱いやすいからで、ここに当然ながら誤差が存在する。ざっと覚えておくとよいのは倍精度で8桁位まで有効に働く。10進数の有効数字としては、12桁位まであるんだけど、科学計算したりすると桁落ちが発生するので、経験上8桁までは有効になる。
元ネタが30年前の本を参照しているので、1990年代ぐらい。ちょうど情報科学学科ができ始めた頃で、C 言語が徐々に広まっていたころ。科学計算だと Fortran が主流でまだ一般的なプログラムとしては BASIC が主流だった頃の話だ。90年代としてひとくくりにしてしまうとかなり面倒なんだけど(インターネット接続も含まれるから)、Excel VBA が広まり始めた時期でもある。
メモリとバス幅の制約
ちょうど1990年代は、コンピュータ言語がいろいろできた時期でもあるので、このあたりの背景を説明すると、
- 浮動小数点付きの計算は「高価」で、専用のコプロセッサで動かしていた
- 高価だったから、普通の CPU はライブラリで浮動小数点計算をしていた。ので遅かった。
- まだ、32ビットマシンが出たばかりで、レジスタやバス幅は 32 ビットだった
- バス幅の関係上、単精度(32ビット)は早かったが、倍精度(64ビット)は遅かった。
- ストレージ(フロッピー、HDD)が小さかったので、64ビットを保存するのは勿体なかった
という関係上、実数の計算は主に単精度(float)が使われていた。科学計算を専門に扱う Fortranはデフォルトが倍精度…と思っていたけど real(単精度)ですね。Fortran 入門: 定数と変数 http://www.nag-j.co.jp/fortran/FI_4.html を参照。自分の場合、炉心計算で倍精度にしていたらしい。
BASIC は 90年代よりも前からあるので、実数の場合「単精度」が使われている。なので、表現上は8桁位でるのだが、計算を繰り返しているうちに有効桁数は4桁位になってしまう。
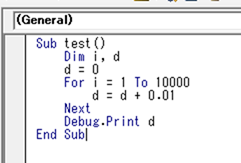
これが1万回くりかえすと…の話になる。
ちなみに、Excel 2013 の VBA を使って計算をすると以下の計算は、100.000000000014 になる。デフォルトで倍精度(double)になっている。
実運用上問題はないけど、これを 100.00 と比較すると「偽」になる。当然だ。実数の比較するときには、先の xUnit の例で述べた通り有効範囲を指定しないとダメだからだ。
加算の繰り返しで誤差が累積する
先の計算で、手っ取り早く誤差をうまないためには「実数を整数の範囲に直す」という計算方法が使われる。科学計算の場合は有効桁数で済ませられるのだが、金融関係ではそれではダメだったりする。お金の問題は最後の1円まで有効になる。
お金の計算はいくつか特殊で、
- 消費税で円以下は切り捨て
- 為替計算では銭単位まで計算(だったとはず)
- 利息では銭まで計算
- 利子は円で切り捨て
- 四捨五入ではなく銀行まるめを使う
という特有なルールがある。なので、0.01ドル(1セント)のような小数点以下2桁までは重要だったりする。これが1万回加算されたとき(積み立てたとき?)に100.00ドルぴったりにならないと困るわけだ。
最近のシステムでは、decimal や money などのお金を扱うための型が用意されているが(中身も10進数で計算する)、90年代にはそういうものがなかったので、COBOL のように10進数計算ができるプログラム言語を使うか、自前で作るしかなかった。
ただし、0.01 単位というのが分かっていれば、手っ取り早く 100 倍して整数に直し、結果を100で割ればよい。
な感じに書き換えると、答えは「100.00」ぴったりになる。
浮動小数点をコンピュータで扱うと有効桁以下のところの誤差が当然でてくる。これを100回加算すれば2桁誤差が増えるし、1万回加算すれば4桁誤差が上がってくる。なので、実数をあつかうときに注意しないといけないのは、
- 有効桁数
- 小数点以下の固定の桁数
とは違うということだ。ソフトウェア工学の教科書の最初に出てくる問題なので「教養」の範疇だと思うし、統計をコンピュータ処理するときの常識=「知っておくべき知識」だと思うのだが、どうだろうか?
有効桁数はよく聞かれるので、有効桁数4桁といえば「1234000」な形や「1.234」な形で示される数字の部分だ。小数点以下でゼロをつけるて明示的に「1.000」として有効桁数を表す場合も多い。
これと混同しやすいのは、小数点以下の固定の桁数で「100.234」みたいな形のもの。有効桁数は6桁と考ええても良いけど、この場合は小数点以下の桁数のほうが重要で、固定小数点で小数点以下3桁有効、という言い方をする。浮動小数点は指数表示で表してもいいけど(有効桁数のほうが重要なので)、固定小数点の場合は小数点以下の桁数が重要になるので指数表現するとまずい場合が多い。
100.234 の表現の場合、100 の回りに値が散らばっていて 101.000 とか、98.123 とかの値があるということだ。この場合、測定値から 100.00 を引いてやれば、桁あふれの危険がすくなくなる。0.234 とか 1.000 とか –2.123 とかにならうからだ。これだと有効桁数もわかりやすい。
統計を計算するときに、平均とか分散を計算するのだが、単純に測定値を加算していくつ桁あふれをしてしまう。1万位なら大したことがないとおもうだろけど、100万件のデータの平均を出すときに単純に加算してしまうと桁あふれ(オーバーフロー)を起こしてしまうのは明白だ。だから、先のように 100 の周辺に値が集まっている(身長などはそれ)場合には、だいたい平均っぽい値を先に引いてしまう。これを「ドメイン知識」という(というのを心理統計法で最近知った)。いわゆる、統計をとったときの特性(ドメイン知識)がないと単純に加算してオーバフローを起こすか誤差を累積させてしまうが、適度な知識があれば、誤差を抑えて精度のよい計算ができる。
物理的な有効桁数は意外と少ない
キログラム原器から プランク定数 をもとに計算するように変わったわけだが、プランク定数 6.626 070 040(81)×10-34 J s の桁数がそのまま計測値に適用できるわけではない。というか、たくさんの桁数があっても意味はない(測定誤差があるので)。
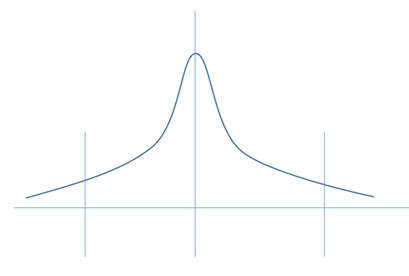
なので、測定誤差も含めて材料力学では2,3桁の有効数字で十分だし(安全係数が、1.2 のように実質小数点以下1桁ぐらいなのから推測できる)、天文学に至っては log で計算してしまうので1桁あれば十分だったりする。そもそも、物理の世界では、値が倍ぐらい違ってもびくともしないので、有効桁数は0.5桁という、有効桁数が小数点以下という感覚もある。電子工学でも抵抗の値は10%位の誤差を許容する(誤差自体が書いてある)し、温度や湿度、電流によって特性グラフがデータシートとしてあるので、ぴったりとした値が決められる訳ではない。むしろ、誤差なり特性なりを含む許容範囲が必要となる。
こんな感じに、値が分布していて許容できる上限下限を決める。部品や測定値は真ん中に集中する(正規分布など)グラフになる。
なので、計算誤差が累積したり測定誤差があったりするのを前提として、この範囲内で「正しい計算」を使用とするのが科学計算である。だから、実数を扱う場合と整数を扱う場合はちょっと違うことを意識しないといけない。
乗除算でも誤差を減らすためのテクニックがあって、
- A / B * C
- A * C / B
この2つの答えは同じように見えるが、後者の「A * C / B」のほうが精度がよく計算できる。前者のように割り算を先にやってしまうと、割り切れない場合があるので誤差がでる。それを次の C を掛けることで増幅させているのだ。だから、数値のオーバーフローに注意してという前提はあるが、A * C で誤算なく乗算をした後に、B で割る(割ったとき割り切れなくてよい)という式変形をする。
数式上(無限に有効桁数があると考えらる)では同じだが、コンピュータ上の有限な有効桁数があると制限がでてくるという話である。
p値(有意確率)と誤差伝播
一気に統計値の話になって、AI な話に振っていきたいのだが、この誤差の部分と分布をうまく扱っていかないと、AI で言われるところの「検定」がうまく働かない。学会や論文的には p 値が重要になってくるのだが、測定誤差とか標本分布の確率の話がないのに、一気に p 値にはいってしまうのはどうかと思う…という話を書きたいところなのだけど、まだそこまで勉強が至っていないので今回は割愛。誤差伝播に関しては、隠れマルコフモデル(HMM)で画像解析をやろうとした時期があって、ベイズは少し慣れているんだが。
プロジェクト管理手法の優位性検定とか不具合検出の標本分布とかは計算しておきたいところ。それはまた後日。